탐색 : 주어진 조건을 만족하여 데이터를 찾아내기

완전탐색 =  브루트포스(brute-force) 알고리즘

컴퓨터를 믿고(1초에 1억번 계산) 일일이 전부 무식하게 계산

*시간 복잡도를 먼저 계산해보기!

사진 누르면 백준

import sys
input = sys.stdin.readline

ans=0
r,c=map(int,input().split())
arr=[]
for _ in range(r):
    arr.append(list(map(int,input().split())))
t=int(input())

noise=[]
for i in range(r-2):
    for j in range(c-2):
        noise=sorted(arr[i][j:j+3]+arr[i+1][j:j+3]+arr[i+2][j:j+3])
        if noise[4]>=t:
            ans+=1
            
print(ans)

이 정도 수준의 믿음...!

 

 

완전탐색(백트래킹) => 재귀함수

: 무식하게 찾으려다 조건에 맞지 않으면 뒤로 돌아갈 줄도 알기

 

# 순열/조합 연습코드

- 아래 코드는 오름차순 출력

- 중복되면 안될 때 -> visited 배열에서 체크!

- 조합/순열 -> start를 만들어서 그 뒤로만 세면 조합! = 앞에 있던 수를 절대 넣지 않기...

# 비중복 순열
n, m = map(int,input().split()) # n에서 m개 뽑기
arr=[0 for i in range(m)] # 한 세트가 저장되는 리스트
visited = [False for i in range(n)] # 방문했는지

def recur(cur): 
    if cur == m: # cur : 뽑은 개수, 다 뽑았음 출력 
        print(*arr)
        return
    
    for i in range(n):
        if visited[i]: # 이미 방문했으면 건너뛰기
            continue
        
        arr[cur] = i+1 # 이번 자리수는 i
        visited[i] = True # 방문 했음
        recur(cur+1) # 다음 자리수 찾기
        visited[i] = False # 다시 되돌리기

recur(0) # 아직 0개 뽑았어요

>>> 4 2

 

# 비중복조합
n,m=map(int,input().split()) # n에서 m개뽑기
arr=[0 for i in range(m)] # 조합 한 세트 저장
visited = [False for i in range(n)] # 방문기록

def recur(cur, start): # cur : 뽑은 개수, start : 조합시작숫자
    if cur == m: # 다 뽑았으면 출력
        print(*arr)
        return

    for i in range(start, n): # s부터 n까지 반복
        if visited[i]: # 방문했으면 넘기기
            continue
        visited[i]=True 
        arr[cur] = i+1 # 지금자리에 이 숫자
        recur(cur + 1, i + 1) # 뽑은수 올리기, start수를 올려야 그 start와 그 뒤의 숫자들끼리의 조합이 나옴.
        visited[i]=False
recur(0,0)

>>> 5 3

 

# 중복 순열
n, m = map(int,input().split()) # n에서 m개 뽑기
arr=[0 for i in range(m)] # 한 순열 저장

def recur(cur):
    if cur == m: # 한 세트 다 뽑았으면 출력
        print(*arr)
        return
    
    for i in range(n): # n개의 수 전부 돌아가면서 서봐!
        arr[cur] = i+1
        recur(cur+1) # 그 다음자리수도!
        
recur(0)

>>> 4 2

 

# 중복 조합
n, m = map(int, input().split()) # n에서 m개 뽑기
arr = [0 for i in range(m)] # 한 세트 조합 저장

def recur(cur, start): # cur : 뽑은 개수, start : 이 수를 포함하여 이 뒤의 숫자들로 조합!
    if cur == m: # 다 뽑았으면 출력
        print(*arr)
        return
    
    for i in range(start, n): # 현재 숫자부터 n까지 전부 한 번 씩 서봐!
        arr[cur] = i+1 # 이번 숫자는 너야
        recur(cur+1, i) # 뽑은 숫자는 올렸지만, 시작 수는 올리지 않음. 자기 자신도 ㄱㅊ으니까
        
recur(0, 0)

>>> 4 2

 

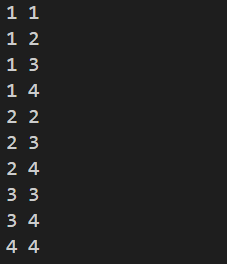
대강 규칙을 알았지? 이 정도는 금방 생각해도 좋겠지만 바로 나올 정도로 반복연습 하자

 

이진탐색 : 중간 선택 후 절반 삭제(업다운)

ex) 1~100에서 임의의 수 x 찾기

- 완전 탐색 O(N)

- 이진 탐색 O(logN)

--> 정렬이 필요하다면 정렬 O(NlogN) 후 이분 탐색

n, x = map(int,input().split()) # 1부터 n까지의 수에서 x 찾기

left = 1
right = n

while left <= right: # 왼<=좌 상태일 경우에만 반복, 아니라면 다 돈 셈이니까
    mid = (left + right) // 2 # 둘의 가운데(더 작은 쪽)
    
    if x < mid:
        right = mid-1
    elif mid < x:
        left = mid+1
    else: # mid == x
        break

print(mid)

 

물론 이 또한 시간복잡도 고려하고 시작

 

 

분할정복

: 어떤 문제를 최소로 쪼갠 후 그 하위 문제를 해결하고 다시 합치면서 문제의 답을 도출

- 병합정렬 : 4528 -> 4   5   2   8  ->   45   28   -> 2458

분할 O(logN) + 병합 O(N) => O(NlogN)

# 재귀 잘 따라가면 밑에서부터 쭉쭉 정렬되며 합쳐짐
def merge_sort(arr): # 분할
    if len(arr) <=1:
        return arr
    
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]
    
    left = merge_sort(left)
    right = merge_sort(right)
    
    return merge(left, right) # 가장 아래서부터 합치기

def merge(left, right): # 병합하며 정렬
    result = []
    i = 0
    j = 0
    
    while i < len(left) and j < len(right): # 왼 전부와 오른 전부를 각각 비교
        if left[i] < right[j]: # 더 작은 걸 넣기
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    # 다 비교하고 남는 애들은 우르르 넣기
    while i < len(left):
        result.append(left[i])
        i += 1

    while j < len(right):
        result.append(right[j])
        j += 1

    return result

print(*merge_sort(list(map(int,input().split()))))